TUGAS KULIAH MATEMATIKA DISKRIT
Nama : Yunita Arfiani
Kelas : 1D Teknik Informatika
NIM : 1801301074
Matkul : Matematika diskrit
Semester : 1
MATERI FUNGSI
Fungsi
Fungsi adalah relasi atau hubungan yang memasangkan setiap anggota himpunan daerah asal (domain) tepat satu, ke himpunan daerah kawannya (kodomain). Setiap anggota himpunan daerah asal mempunyai pasangan,dan hanya tepat satu dipasangkan dengan daerah kawannya. Setiap fungsi pasti merupakan relasi.
Suatu fungsi f dari himpunan A ke himpunan B adalah suatu relasi yang memasangkan setiap elemen dari A secara tunggal dengan elemen pada B. Apabila f memetakan suatu elemen x di A ke suatu y di B ini dinyatakan dengan notasi f(x), dan biasa ditulis dengan f : x relasi f(x), sedangkan x biasa disebut prapeta dari f(x).
Domain, kodomain dan range
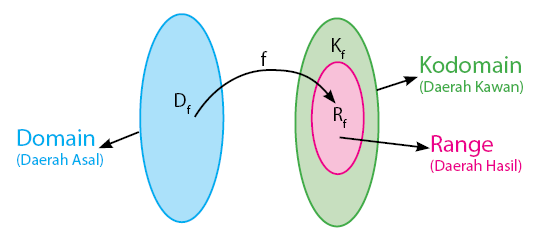
Domain adalah daerah asal, kodomain adalah daerah kawan, himpunan nilai yang diperoleh dari relasi antara domain dan kodomain tersebut disebut daerah hasil atau range.
Jenis jenis fungsi
A). Fungsi KonstanSuatu fungsi f : A relasi B ditentukan dengan rumus f(x) disebut fungsi konstan. Apabila untuk setiap anggota domain fungsi selalu berlaku f(x) = C, di mana C bilangan konstan/dengan nilai tetap. Fungsi konstan disebut juga fungsi tetap. Contoh : f(x) = 3, maka Rf = 3.
B).Fungsi Polinomial
Polinom atau suku banyak disebut dengan polinom, merupakan bentuk suku suku dengan nilai banyak yang disusun dari perubah variabel dan konstanta. Operasi yang digunkan hanya penjumlahan, pengurangan, perkalian dan pangkat bilangan bulat tak negative. Contoh :
A : {1, 2, 3}
B : {2, 5, 7, 10}
B : {2, 5, 7, 10}
f(x) : x2 + 1
Jadi,
f(1) : 12 + 1 = 2
f(2) : 22 + 1 = 5
f(3) : 32 + 1 = 10
Rf : {2, 5, 10}
C). Fungsi Pangkat
fungsi yang variabel bebasnya berpangkat sebuah bilangan nyata bukan nol. y = xn ; n = bilangan nyata bukan nol.
fungsi yang variabel bebasnya berpangkat sebuah bilangan nyata bukan nol. y = xn ; n = bilangan nyata bukan nol.
Contoh :
x : {Bilangan bulat positif <3}
y : {1, 2, 3, 4}
f(x) : 2x
Jadi,
x : {1, 2}
f(1) : 21 = 2
f(2) : 22 = 4
Rf : {2, 4}
D). Fungsi Floor dan Ceiling
Misalkan x adalah bilangan riil, berarti x berada diantara dua bilangan bulat.
Fungsi floor dari x:
[x] menyatakan nilai bilangan bulat terbesar yang lebih kecil atau sama dengan x
Fungsi ceiling dari x:
[x] menyatakan bilangan bulat terkecil yang lebih besar atau sama dengan x
Fungsi floor dari x:
[x] menyatakan nilai bilangan bulat terbesar yang lebih kecil atau sama dengan x
Fungsi ceiling dari x:
[x] menyatakan bilangan bulat terkecil yang lebih besar atau sama dengan x
Dengan kata lain, fungsi floor membulatkan nilai x ke bawah, sedangkan fungsi ceiling membulatkan nilai x ke atas.
Contoh nilai fungsi floor dan ceiling :

E). Fungsi Identitas
Fungsi R relasi R yang didefinisikan sebagai f : x relasi x disebut fungsi identitas.
Sifat sifat fungsi
A). Fungsi Injektif (satu satu)
Fungsi f : A→ B dikatakan fungsi satu satu, jika setiap elemen himpunan A mempunyai pasangan tepat dan hanya 1 yang tidak sama pada elemen himpunan B. Contoh :

B). Fungsi Surjektif (Pada)
Fungsi f : A→ B dikatakan fungsi pada, jika setiap elemen himpunan B muncul sebagai pasangan dari sekurang- kurangnya satu elemen himpunan A. Dan jika setiap elemen himpunan B merupakan pasangan dari satu atau lebih elemen himpunan A. Contoh :

C). Fungsi Bijektif (Korespondensi)
Fungsi f : A→ B dikatan fungsi bijeksi jika sebuah fungsi yang merupakan fungsi satu satu (Injektif) maupun fungsi pada (Surjektif).

Ekuivalen fungsi
Suatu fungsi dinyatakan ekuivalen jika, f = g / f(x) = g(x). Artinya fungsi f(x) dan fungsi g(x) sama atau memiliki keterkaitan satu sama lain. Contoh :
Diketahui : f(x) : 2x
A :{1, 2, 3}
B : {Bilangan asli kurang dari = 10}
Rf : {2, 4, 8}
Berdasarkan hasil fungsi f(x) diatas, apakah f ekuivalen dengan g. jika diketahui g : A relasi B, g : {x | = 2 . 2x-1}
Cara 1 dengan membuktikan range nya.
g : {x | = 2 . 2x-1} dapat di tulis menjadi g(x) : 2 . 2x-1
Kemudian masukkan masing masing variabel domain A, kedalam setiap fungsi x.
g(1) : 2 . 21-1 = 2
g(2) : 2 . 22-1 = 4
g(3) : 2 . 23-1 = 8
Rg : {2, 4, 8}
Hasil nya terbukti f = g, karena Rg nya memiliki hasil yang sama. Jadi, f dan g adalah ekuivalen.
Cara 2 dengan membuktikan nilai fungsi f(x) nya.
g(x) : 21 . 2x-1
: 21 + x - 1
: 2x = f(x)
(tuliskan rumus yang ada pada soal, angka dua yang sebelumnya tidak ada pangkat memiliki pangkat 1, karena jika suatu bilangan yang tidak memiliki pangkat, dianggap memilki pangkat 1, jadi bisa dituliskan seperti contoh di atas untuk memudahkan pengerjaan)
(Pada tahap selanjutnya menggunakan cara coret, dengan mencoret angka 1).
Invers fungsi
Jika f adalah fungsi berkoresponden satu-ke-satu dari A ke B, maka kita dapat menemukan balikan (invers) dari f, karena hanya fungsi yang berkorespondensi satu satu saja yang dapat dicari inversnya. Balikan fungsi dilambangkan dengan f-1. Misalkan a adalah anggota himpunan A dan b adalah anggota himpunan B, maka f-1(b) = a jika f-1(a) = b. Fungsi yang berkoresponden satu-ke-satu sering dinamakan juga fungsi yang invertible (dapat dibalikkan), karena kita dapat mendefinisikan fungsi balikannya. Sebuah fungsi dikatakan not invertible (tidak dapat dibalikkan) jika ia bukan fungsi yang berkoresponden satu-ke-satu, karena fungsi itu tidak dapat dibalikkan.
Dapat disimpulkan bahwa daerah hasil dari f-1 (x) merupakan daerah asal bagi f(x) begitupun sebaliknya. Contoh :
Carilah invers fungsi f jika f : bilangan bulat, dengan f(n) : n+2
f(n) : n+2
n : f(n) - 2
f-1(n) : n-2
Contoh lain :

Komposisi fungsi
Misalkan g adalah fungsi dari himpunan A ke himpunan B, dan f adalah fungsi dari himpunan B ke himpunan C. Komposisi f dan g, dinotasikan dengan f o g, adalah fungsi dari A ke C yang didefinisikan oleh (f o g)(a) = f(g(a)).
(g o f)(x) artinya f dimasukkan ke g.
(f o g)(x) artinya g dimasukkan ke f.
Fungsi komposisi memiliki beberapa sifat, diantaranya:
Tidak Komutatif
(g o f)(x) = (f o g)(x)
Asosiatif
(f o (g o h))(x) = ((f o g) o h)(x)]
Fungsi Identitas I(x) = x
(f o I)(x) = (I o f)(x) = f(x)
Contoh Soal :
Diketahui f(x) = 3x - 4 dan g(x) = 2x, maka tentukanlah rumus (f o g)(x) dan (g o f)(x) ...
Jawab:
(f o g)(x) = g dimasukkan ke f menggantikan x
(f o g)(x) = 3(2x)-4
(f o g)(x) = 6x - 4
(g o f)(x) = f dimasukkan ke g menggantikan x
(g o f)(x) = 2(3x-4)
(g o f)(x) = 6x-8
Daftar pustaka :
Amir, Muhammad Faizal, Prasojo, Bayu Hari, 2016, "Buku ajar matematika dasar", Jl. Mojopahit 666 B Sidoarjo : UMSIDA PRESS.
Munir, Rinaldi, 2010, "Matematika diskrit edisi 3 revisi keempat", Bandung : Informatika Bandung.
https://www.madematika.net/2015/08/jenis-jenis-fungsi-dan-sifat-sifat.html
http://www.rumusmatematikadasar.com/2015/01/pembahasan-fungsi-komposisi-dan-fungsi-invers.html
http://www.rumusmatematikadasar.com/2015/01/pembahasan-fungsi-komposisi-dan-fungsi-invers.html


0 komentar:
Posting Komentar